Multi-objective optimization
We developed the first-of-a-kind TEMOA version that allows for multi-objective optimization (MOO), which is available at [1]. It builds upon the extended version of TEMOA developed within the MAHTEP group [2] and includes the MOO as an additional module, as schematized in Figure 1.
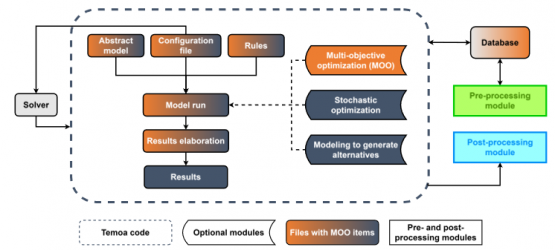
Figure 1. Scheme of the TEMOA modeling framework updated with the additional MOO items [1].
The MOO is activated through the configuration file, while the steps for solving the MOO are defined in the “temoa_run” file, which includes the execution code of the model. These steps call the equations defined in the “temoa_moo” file, which in turn imports the objective functions from “temoa_model” and “temoa_rules” files.
The current and unique MOO method included in the module is the Augmented epsilon-constraint (AUGMECON) method [3]. It is a well-established method, which was developed as a reformulation of the epsilon-constraint method to ensure Pareto optimality. A solution to a MOO problem is considered Pareto optimal if improving one objective leads to the deterioration of another [3]. Let’s consider the minimization of multiple objective functions. The AUGMECON method transforms all but one objective into equality constraints. Except for the latter, each objective is first minimized individually to determine the boundaries of the Pareto front. Then, a desired number and distribution of caps within the Pareto front boundaries are selected. Finally, the MOO is solved for all the chosen caps, yielding Pareto-optimal solutions to the original MOO problem.
The AUGMECON method is comprehensively described in [3]. The first application in TEMOA was done in [4] while for applications to other ESOMs, see e.g., [5], [6], [7].
References
- MAHTEP Group, “MAHTEP/TEMOA/moo - Release 1.0,” GitHub. Accessed: Jun. 19, 2024. [Online]. Available: https://github.com/MAHTEP/TEMOA/releases/tag/moo1.0
- MAHTEP Group, “MAHTEP/TEMOA,” GitHub. Accessed: Oct. 28, 2023. [Online]. Available: https://github.com/MAHTEP/TEMOA
- G. Mavrotas, “Effective implementation of the e-constraint method in Multi-Objective Mathematical Programming problems,” Appl Math Comput, 2009, doi: 10.1016/j.amc.2009.03.037.
- G. Colucci, V. Bertsch, V. Di Cosmo, J. Finke, and L. Savoldi, “Combined assessment of material and energy supply risks of the energy transition: a multi-objective energy system optimization approach,” Submitted to Applied Energy, 2024.
- J. Finke and V. Bertsch, “Implementing a highly adaptable method for the multi-objective optimisation of energy systems,” Appl Energy, 2023, doi: 10.1016/j.apenergy.2022.120521.
- S. Pathe and V. Bertsch, “Combining Life Cycle Assessment and Energy System Optimization to Model Sustainable Power Systems Transformation,” in Energy Proceedings, 2022. Accessed: May 11, 2024. [Online]. Available: https://www.energy-proceedings.org/combining-life-cycle-assessment-and-energy-system-optimization-to-model-sustainable-power-systems-transformation/
- D. Huckebrink, J. Finke, and V. Bertsch, “How user behaviour affects emissions and costs in residential energy systems-The impacts of clothing and thermal comfort,” Environ. Res. Commun, vol. 5, p. 115009, 2023, doi: 10.1088/2515-7620/ad0990.

